Экзамен в ШАД 2016. Некоторые решения.

Как-то раз мы с Медленной Пандой решили порешать задания из вступительного экзамена в ШАД Яндекса за 2016 год. Из этого вышло примерно нижеперечисленное. Если найдете ошибки, обязательно дайте знать в комментариях или любым другим удобным вам способом.

№1

Условие: Пусть \(A\) и \(B\) – квадратные ненулевые матрицы одинакового размера. Верно ли, что если \(ABA=A\), то \(BAB=B\)?

Решение: Возьмем следующие матрицы: \(A=\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\), \(B=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\). Они удовлетворяют всем требованиям из условия, \(ABA=\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}=A\), но при этом \(BAB=\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}=A\). Следовательно, утверждение неверно.

№2

Условие: Исследуйте на сходимость ряд \[\sum_{n=3}^{\infty}(\ln\ln n)^{-\ln n}.\]

Решение: Все члены ряда положительные, следовательно, можно воспользоваться предельным логарифмическим признаком сходимости: \(\lim_{n\to\infty}\frac{\ln \frac{1}{a_{n}}}{\ln n} \)
\( = \lim_{n\to\infty}\frac{\ln ((\ln\ln n)^{-\ln n})^{-1}}{\ln n} \)
\( = \lim_{n\to\infty}\frac{\ln (\ln\ln n)^{\ln n}}{\ln n} \)
\(=\lim_{n\to\infty}\frac{(\ln n)\cdot\ln\ln\ln n}{\ln n} \) \( = \lim_{n\to\infty}\ln\ln\ln n \)
\( = \infty\)

Поскольку предел больше единицы, исследуемый ряд сходится.

№3

Условие: Случайные величины \(X\) и \(Y\) независимы. Плотность случайной величины \(X\) равна \(p_{X} (t) = \frac{t}{2}\cdot I_{[0;2]} (t)\) (где \(I_{[0;2]} (t)\) – индикаторная функция отрезка \([0;2]\)), а \(Y\) имеет равномерное распределение на отрезке \([0;3]\)). Найдите вероятность того, что из отрезков с длинами \(X\), \(Y\) и \(1\) можно составить треугольник.

Update 14.07.2018: Спасибо Павлу Коробову за найденную ошибку и наводку. Решение исправлено.

Решение: Возможность составить треугольник эквивалентна выполнению неравенства треугольника для каждой из сторон. Получается, что
\( P\{\Delta\} \)
\( =P\{X+Y>1,\ X+1>Y,\ Y+1>X\} \)
\(\xcancel{=P\{X+Y>1\}\cdot P\{X+1>Y\}\cdot P\{Y+1>X\}}\).

\(X\) и \(Y\) по условию независимы, следовательно, из их плотностей можно составить совместную плотность простым умножением: \(p_{X,Y}(t,z) = p_{X}(t) \cdot p_{Y}(z) \).

Введем случайную величину \(\xcancel{ \eta =X+Y }\). Положим \(\xcancel{D_s \subset \mathbb{R}^2: (t,z) \in D_s \iff t+z < s }\). Таким образом,
\(\xcancel{F_{\eta }(s)}\)
\(\xcancel{=\iint_{D_s} p_{X,Y}(t,z) \mathrm{d} t \mathrm{d} z }\)
\(\xcancel{=\iint_{D_s} p_{X}(t) \cdot p_{Y}(z) \mathrm{d}t \mathrm{d}z }\).

\(\xcancel{P\{X+Y>1\}}\)
\(\xcancel{=1-P\{X+Y<1\}}\)
\(\xcancel{=1-F_{\eta }(1)}\)
\(\xcancel{=1-\iint_{D_1} p_{X}(t) \cdot p_{Y}(z) \mathrm{d}t \mathrm{d}z}\)
\(\xcancel{=1-\int_{-\infty}^{+\infty} ( \int_{-\infty}^{1-z} p_{X}(t) \cdot p_{Y}(z) \mathrm{d}t ) \mathrm{d}z}\)
\(\xcancel{=1-\int_{-\infty}^{+\infty} ( \int_{-\infty}^{1-z} \frac{t}{2} I_{[0;2]}(t) \cdot p_{Y}(z) \mathrm{d}t ) \mathrm{d}z}\)
\(\xcancel{=1-\int_{0}^{3} ( \int_{-\infty}^{1-z} \frac{t}{2} I_{[0;2]}(t) \cdot \frac{1}{3} \mathrm{d}t ) \mathrm{d}z}\)
\(\xcancel{=1-\int_{0}^{1} ( \int_{0}^{1-z} \frac{t}{2} \cdot \frac{1}{3} \mathrm{d}t ) \mathrm{d}z}\)
\(\xcancel{=1-\int_{0}^{1} \frac{(1-z)^2}{12} \mathrm{d}z}\)
\(\xcancel{=\frac{35}{36}}\)

Аналогично получаем, что \(\xcancel{P\{X+1>Y\} = \frac{7}{9}}\) и \(\xcancel{P\{Y+1>X\} = \frac{31}{36}}\). В итоге \(\xcancel{P\{\Delta\}=\frac{7595}{11664}\approx 0.65}\).

Построим область, в которой выполняется неравенство треугольника для сторон \(X\), \(Y\) и \(1\). Дополнительно отсечем ту ее часть, которая соответствует нулевой плотности распределения \(X\) или \(Y\).

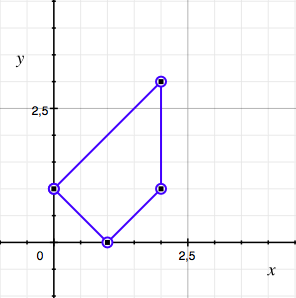
Чтобы получить ответ, проинтегрируем совместную плотность распределения \(X\) и \(Y\) по построенной области. При этом учтем, что индикаторная функция из плотности \(X\) на построенной области всегда будет давать единицу, а плотность \(Y\) постоянна и равна \(\frac{1}{3}\).

\( P\{\Delta\} \)
\( =\int_{0}^{2} ( \int_{0}^{t+1} p_{X}(t) \cdot p_{Y}(z) \mathrm{d}z ) \mathrm{d}t \)
\(- \int_{0}^{1} ( \int_{0}^{-t+1} p_{X}(t) \cdot p_{Y}(z) \mathrm{d}z ) \mathrm{d}t \)
\(- \int_{1}^{2} ( \int_{0}^{t-1} p_{X}(t) \cdot p_{Y}(z) \mathrm{d}z ) \mathrm{d}t\)
\( =\int_{0}^{2} ( \int_{0}^{t+1} \frac{z}{6} \mathrm{d}z ) \mathrm{d}t - \int_{0}^{1} ( \int_{0}^{-t+1} \frac{z}{6}) \mathrm{d}z ) \mathrm{d}t - \int_{1}^{2} ( \int_{0}^{t-1} \frac{z}{6} \mathrm{d}z ) \mathrm{d}t \)
\( = \frac{7}{9} - \frac{1}{36} - \frac{5}{36} \)
\( = \frac{11}{18} \)
\( \approx 0.61 \)

№5

Условие: Существует ли непрерывная функция \(f(x)\), для которой \(f(f(x)) = 1-x^3\)?

Решение: \(f(f(x))\) строго монотонно убывает; про \(f(x)\) можно утверждать следующее:

1) \(f(x)\) не константа, иначе \(f(f(x))\) как композиция функций-констант была бы константой, что противоречит строгой монотонности \(f(f(x))\)

2) \(f(x)\) строго монотонна: пусть не так, тогда у \(f(x)\) существует хотя бы один локальный максимум(минимум). В точке локального максимума(минимума) \(f(x)\) функция \(f(f(x))\) будет иметь локальный минимум(максимум), что противоречит строгой монотонности \(f(f(x))\)

3) \(f(x)\) не возрастающая функция, так как композиция возрастающих функций есть возрастающая функция, что противоречит тому, что \(f(f(x))\) убывает

4) \(f(x)\) не убывающая функция, так как композиция убывающих функций есть возрастающая функция, что, аналогично, противоречит тому, что \(f(f(x))\) убывает

Таким образом, \(f(x)\) – строго монотонная функция, которая при этом не может ни возрастать, ни убывать, что позволяет сделать вывод о том, что такую функцию построить невозможно.

№6

Условие: В ряд расположены \(m\) предметов. Случайно выбираются \(k\) предметов, \(k < m\). Случайная величина \(X\) равна количеству таких предметов \(i\), что \(i\) выбран, а все его соседи не выбраны. Найдите математическое ожидание \(X\).

Решение: Представим случайную величину \(X\) как сумму случайных величин \(x_{i}\):
\[ x_{i} =
\begin{cases}
1 & \quad i \text{-й выбран, соседи – нет}\
0 & \quad \text{в остальных случаях}\
\end{cases}
\]
Таким образом, \(М[X]\)
\(=M[\sum_{i=1}^{m}x_i]\)
\( = \sum_{i=1}^{m}M[x_i]\)
\(=\sum_{i=1}^{m}1\cdot P\{x_i=1\} \)
\(= \sum_{i=1}^{m} P\{x_i=1\} \)

Крайние левый и правый предметы имеют лишь по одному соседу, поэтому их следует рассмотреть отдельно. Соответствующие вероятности считаются простым произведением:

\( P\{x_{i}=1\} \)
\(=
\begin{cases}
\frac{k}{m} (1-\frac{k-1}{m-1}) & \quad i=1,m \
\frac{k}{m} (1-\frac{k-1}{m-1}) (1-\frac{k-1}{m-2}) & \quad i\neq 1,m\
\end{cases}
\)

После подстановки и преобразований получаем ответ:
\[М[X]=\frac{k(m-k)(m-k+1)}{m(m-1)}.\]